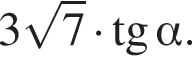Среди выражений (−1)4; ![]() 40; (0,4)−1;
40; (0,4)−1; 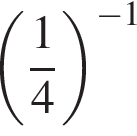 укажите то, значение которого равно 4.
укажите то, значение которого равно 4.
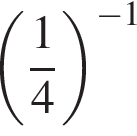
Среди выражений (−1)4; ![]() 40; (0,4)−1;
40; (0,4)−1; 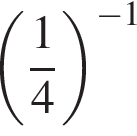 укажите то, значение которого равно 4.
укажите то, значение которого равно 4.
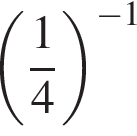
В треугольнике ABC известно, что 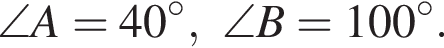 Укажите номер верного утверждения для сторон треугольника.
Укажите номер верного утверждения для сторон треугольника.
На рисунке изображен график движения автомобиля из пункта O в пункт C. Скорость движения автомобиля на участке BC (в км/ч) равна:
Определите, на сколько неизвестное слагаемое меньше суммы, если известно, что x + 20 = 80.
Если  то значение α с точностью до сотых равно:
то значение α с точностью до сотых равно:
Укажите номера функций, для которых значение аргумента, равное −8, является нулем функции.
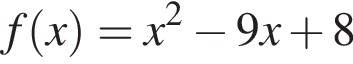


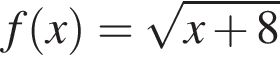
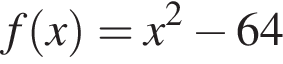
Велосипедист за 6 ч проехал 58 км. За какое время (в минутах) велосипедист преодолеет в полтора раза больший путь, если будет двигаться с той же скоростью?
Найдите сумму всех целых значений функции y = f(x), заданной графиком на промежутке (-5; 5) (см.рис.).
Результат упрощения выражения 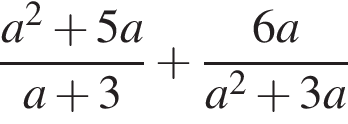 имеет вид:
имеет вид:
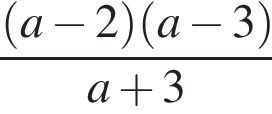
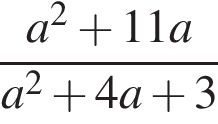
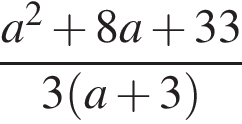
Решением системы неравенств 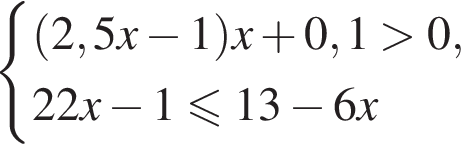 является:
является:
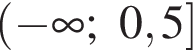
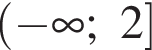


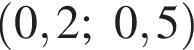
На круговой диаграмме представлена информация о продаже 200 кг овощей в течение дня. Для начала каждого из предложений А — В подберите его окончание 1 — 6 так, чтобы получилось верное утверждение.
А) Масса (в килограммах) проданной капусты равна ...
Б) Отношение, выраженное в процентах, которое показывает, на сколько масса проданного картофеля меньше массы проданных помидоров, равно ...
В) Отношение, выраженное в процентах, которое показывает, на сколько масса проданной свеклы больше массы проданного лука, равно ...
1) 25
2) 40
3) 4
4) 125
5) 38
6) 19
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.
Найдите наибольшее целое решение неравенства 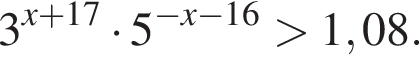
Пусть (x1; y1), (x2; y2) — решения системы уравнений 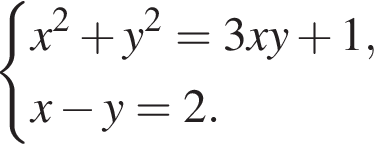
Найдите значение выражения x1x2 + y1y2.
В равнобедренную трапецию, площадь которой равна 115, вписана окружность радиуса 5. Найдите периметр трапеции.
Найдите произведение наименьшего корня (в градусах) на количество различных корней уравнения  на промежутке (−90°; 90°).
на промежутке (−90°; 90°).
Площадь прямоугольника ABCD равна 20. Точки M, N, P, Q — середины его сторон. Найдите площадь четырехугольника между прямыми AN, BP, CQ, DM.
Найдите произведение суммы корней уравнения 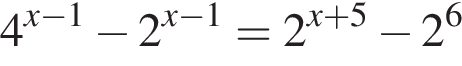 на их количество.
на их количество.
Найдите произведение корней (корень, если он единственный) уравнения 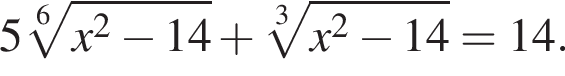
Найдите площадь полной поверхности прямой треугольной призмы, описанной около шара, если площадь основания призмы равна 7,5.
Куб вписан в правильную четырехугольную пирамиду так, что четыре его вершины находятся на боковых ребрах пирамиды, а четыре другие вершины — на ее основании. Длина стороны основания пирамиды равна 1, высота пирамиды — 3. Найдите площадь S поверхности куба. В ответ запишите значение выражения 8S.
Найдите произведение точек минимума функции 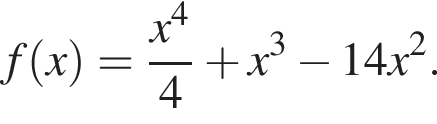
На стороне AB параллелограмма ABCD отмечена точка O так, что 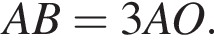 К плоскости ABCD из точки O восстановлен перпендикуляр SO длиной 8. Найдите значение выражения
К плоскости ABCD из точки O восстановлен перпендикуляр SO длиной 8. Найдите значение выражения 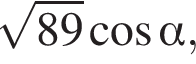 где
где ![]() — линейный угол двугранного угла BSCD, если
— линейный угол двугранного угла BSCD, если 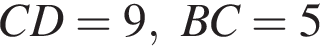 и известно, что площадь ABCD равна 45.
и известно, что площадь ABCD равна 45.
Радиус основания цилиндра равен 13. Плоскость, параллельная оси цилиндра, пересекает цилиндр по прямоугольнику с площадью, равной 108. Найдите значение выражения ![]() где V — объем цилиндра, если расстояние от плоскости сечения до оси цилиндра равно
где V — объем цилиндра, если расстояние от плоскости сечения до оси цилиндра равно ![]()
Равнобедренная трапеция с основаниями длиной 7 и 3 и острым углом 60° вращается вокруг прямой, содержащей ее боковую сторону. Найдите объем тела вращения V и в ответ запишите значение выражения ![]()
Найдите суму всех целых решений неравенства 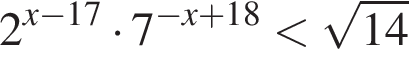 на промежутке (−25; 25).
на промежутке (−25; 25).
ABCA1B1C1 — правильная треугольная призма, все ребра которой равны 6. Точки P и K — середины ребер B1C1 и CC1 соответственно, M ∈ AA1, A1M : A1A = 1 : 3 (см. рис.). Найдите увеличенный в 25 раз квадрат длины отрезка, по которому плоскость, проходящая через точки M, K, P, пересекает грань AA1B1B.
Найдите (в градусах) сумму различных корней уравнения 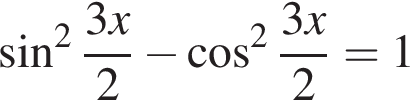 на промежутке
на промежутке 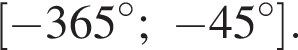
Найдите произведение корней уравнения 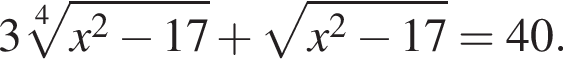
Два крана, работая одновременно, разгрузили баржу за 9 ч. Если бы половину баржи разгрузил первый кран, а затем оставшуюся часть — второй кран, то баржа была бы разгружена за 50 ч. За какое время (в часах) первый кран, работая один, разгрузил бы всю баржу, если известно, что он работает медленнее, чем второй кран?
Основанием четырехугольной пирамиды является ромб, у которого косинус угла равен ![]() и длина стороны равна 16. Все боковые грани пирамиды наклонены к плоскости ее основания под углом α, а высота пирамиды равна 24. Найдите значение выражения
и длина стороны равна 16. Все боковые грани пирамиды наклонены к плоскости ее основания под углом α, а высота пирамиды равна 24. Найдите значение выражения